ویکی‌جزوه/دانشکده:فنی و مهندسی/مکانیک سیالات/نیروی وارد بر سطوح تخت

نیروی هیدروستاتیکی وارد بر سطوح مسطح

هرگاه سطحی در سیال غوطه ور شود از طرف سیال نیروی فشاری به آن وارد می شود. تعیین این نیرو در طراحی سازه های مخازن نگهداری سیال، سدها، کشتی ها و سایر سازه های هیدرولیکی دارای اهمیت بسیار بالایی است.

این نیروها مرتبط با وزن سیالی است که حمل می کند. برای مثال سطح افقی و تخت ته یک مخزن به مساحت A که درون آن آب با عمق H قرار دارد، نیروی فشاری و به سمت پایین $F=\gamma HA$ را تجربه می کند. اگر سطح افقی نباشد، محاسبات اضافی تری لازم است تا مولفه های افقی نیروهای هیدروستاتیکی محاسبه شود.

اگر از تغییرات چگالی صرف نظر شود، و فشار روی هر سطح غوطه‌ور به صورت خطی نسبت به عمق تغییر می‌کند. برای یک سطح مسطح، توزیع تنش خطی دقیقا مشابه ترکیب خمش و فشار در تیرهایی است که در تئوری مقاومت مصالح مطالعه می شوند. بنابراین مسئله هیدروستاتیکی به فرمول ساده‌ای تبدیل می شود که مرتبط با مرکز جرم و گشتاور اینرسی مساحت سطح مقطع صفحه است.

در تعیین نیروهای هیدروستاتیکی وارد بر یک سطح دو چیز مهم است:

۱) مقدار نیروی برآیند

۲) نقطه اثر نیرو

نیروی وارد بر سطح تخت در سیال ساکن

همانطور که در تصویر مشخص است با افزایش عمق آب فشار به صورت خطی افزایش میابد نیروی برآیند در مرکز فشار(cp) که در اثبات پایین به دست آمده است اثر می‌کند. مکان این نیرو با سینوس زاویهٔ بین سطح دریچه وسطح آزاد رابطهٔ مستقیم دارد. این نیرو عمود بر سطح وارد می‌شود.

برای به دست آوردن فرمول های مربوط به اشکال صفحه ای، یک سیستم مختصات xy که مبدا آن بر مرکز جرم صفحه واقع است را در صفحه در نظر بگیرید. هم چنین مختصه ساختگی$\xi$رابه سمت پایین سطح صفحه اختیار کنید. در این صورت مقدار نیروی کل هیدروستاتیکی واردبر یک طرف صفحه برابر است با:

$F=\int pdA=\int (p_a+\gamma h)dA=p_{a}A+\gamma \int hdA$ با یادآوری اینکه$h=\xi \sin \theta$ است و طبق تعریف فاصله مرکز جرم سطح شیبدار از سطح صفحه برابر است با:

${\xi }_{CG}=\frac{1}{A}\int \xi dA$

می توان انتگرال باقی مانده در انتگرال فوق را حل کرد. چون $\theta$ در طول صفحه مقداری ثابت است معادله فوق به معادله زیر تبدیل خواهد شد.

$F=P_{a}A+\gamma \sin \theta \int \xi dA=P_{a}A+\gamma \sin \theta \xi A$ سرانجام یادآوری می شویم که ${\xi }_{CG}\sin \theta =h_{CG}$ برابر با فاصله عمودی از سطح تا مرکز جرم صفحه است،بنابراین $F=P_{a}A+\gamma h_{CG}A=(P_a+\gamma h_{CG}(A)=P_{CG}A$

نیروی وارد بر یک طرف هر صفحه غوطه‌ور در یک سیال یکنواخت برابر است با حاصل ضرب مقدار فشار در مرکز جرم صفحه و مساحت صفحه. این نیرو مستقل از شکل صفحه و زاویه شیب $\theta$ آن می باشد.

فرمول های فشار نسبی

در اکثر موارد از فشار محیط $P_a$ چشم پوشید زیرا بر دو طرف صفحه اثر می کند. برای مثال،طرف دیگر صفحه جدار داخلی یا جدار بیرونی و خشک سد می باشد.در این حالت ، $P_{CG}=\gamma h_{CG}$ بوده موقعیت مرکز فشار به وزن مخصوص بستگی دارد:

الگو:چپ‌چین $F=\gamma h_{CG}A$ الگو:پایان چپ‌چین الگو:چپ‌چین $y_{CP}=-\frac{I_{xx}\sin \theta }{h_{CG}A}$ الگو:پایان چپ‌چین یا $y_{cp}=-\frac{I_{xx}\sin \theta \gamma }{P_{CG}A}$ و $X_{cp}=-\frac{I_{xy}\sin \theta \gamma }{P_{CG}A}$ اگر $sin\theta =0$ باشد می توان گفت مرکز فشار همان مرکز نیرو است

اگر $sin\theta =0$ باشد می توان گفت مرکز فشار همان مرکز نیرو است

$x_{CP}=-\frac{I_{{}_{xy}}\sin \theta }{h_{{}^{CG}}A}$

توجه: در حل مسائلی که سطح در تماس با فشار اتمسفر است، از فشار نسبی استفاده می کنیم چون اگر فشار اتمسفر را هم در نظر بگیریم همان فشار بر روی طرف دیگر سطح عمل می کند و دونیرو برابر و خلاف جهت هم هستند وهمدیگر را خنثی می کنند. بنابراین فشار اتمسفر نقشی در نیروی برآیند ایفا نمی‌کند. در غیر اینصورت مجبوریم از فشار مطلق استفاده کنیم.

نتکه: در یک سیال ساکن :

تغییرات فشار در جهت قایم خطی است و تغییرات فشار در جهت افقی صفر است.

نکته: هر جا به جای یک سیال چند لایه سیال داشته باشیم شیب توزیع فشار هیدرواستاتیک در لایه های مختلف فرق داشته و برای سیال چگال تر دارای شیب تند تری است و با توجه به اینکه لایه های سیال به ترتیب افزایش چگالی از بالا به پایین قرار میگریند شیب توزیع فشار از بالا به پایین تند تر میشود.

---

مثال۱

H چه قدر باشد تا سد برگردد؟ الگو:چپ‌چین

الگو:پایان چپ‌چین

الگو:سخ در جهت ساعتگرد گشتاور می گیریم اگر مثبت شد سد می افتد،ولی اگر مقدار گشتاور صفر شد یعنی در استانه افتادن است و اگر مقدار گشتاور منفی شد،پایدار است و نمی افتد. الگو:سخ الگو:چپ‌چین

$\begin{array}{cc}& +\searrow M_A=\frac{1}{3}HF-\frac{2}{3}w=0\\ & F=p_{C.G}A=\gamma \frac{H}{2}Hk\\ & w={\rho }_{s}g\times 5k=S.G.\times \gamma \times 5k\to \frac{1}{3}\gamma \frac{H^3}{2}k=25k\gamma \times \frac{2}{3}\to H=\sqrt[3]{100}\\ \end{array}$

---

مثال۲

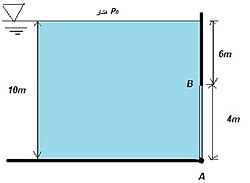
دریچه ای AB (عمود بر صفحه کاغذ) با عرض ۵ متر و به وزن ۱ کیلو نیوتون است. دریچه در B آزاد و A لولا شده است. فاصله B تا سطح آزاد ۶ متر و و A تا سطح آزاد ۱۰ متر است. نیروهای وارد بر دریچه در نقاط A و B را بدست آورید.

الگو:سخ جواب : الگو:سخ

در نقطه Bهیچ نیرویی وارد نمیشود.چون دریچه در Bآزاداست.

نیروی وارد بر دریچه از طرف سیال را بدست می آوریم وسپس از تعادل استاتیکی نیرو در لولا را بدست می آوریم.

نیروی وارد بر دریچه از طرف سیال را می توان از دو روش مشابه بدست آورد :

روش اول : با استفاده از فشار در وسط دیوار:
الگو:چپ‌چین $F=P_{CG}A=\rho g{h}_{CG}A=1000\times 9.81\times 8\times 20=1569.6kN$

الگو:پایان چپ‌چین روش دوم با استفاده از مساحت ذوزنقه توزیع فشار : الگو:چپ‌چین $F=(\frac{P_1+P_2}{2})hb=(\frac{\rho h_1+\rho h_2}{2})hb=(\frac{1000\times 9.81\times (6+10)}{2})(8\times 20)=1569.6kN$
الگو:پایان چپ‌چین بنابراین طبق تعادلات استاتیکی داریم:

الگو:چپ‌چین $sum{F}_X=0\Rightarrow F-A_X=0\Rightarrow F=A_X\Rightarrow A_X=1569.6kN$

$sum{F}_Z=0\Rightarrow A_Z-W=0\Rightarrow A_Z=W\Rightarrow A_Z=1kN$ الگو:پایان چپ‌چین

---

نیروی وارد بر سطوح تخت مایل در سیال ساکن

مثال۳

در شکل زیر دریچه مثلثی شکلی(متساوی الساقین) قرار دارد(دریچه CDE). این دریچه حول لولای CD حرکت میکند. برای بازشدن دریچه باید نیروی p به طور عمودی بر نقطه E اعمال شود. در داخل ظرف مایعی به چگالی $0.8\times {10}^3\frac{kg}{m^3}$ قرار دارد و پابین دریچه هوای آزاد است. با صرف نظر کردن از وزن دریچه:

الف) نیروی فشاری وارد بر دریچه(عمود بر سطح دریچه) را بدست آورید.

ب) مرکز فشار را بدست آورید.

ج) مقدار نیروی لازم p وارد برنقطهٔ E برای باز کردن دریچه را بدست آورید.

پرونده:1234567.png

الف)

$\overline{Y}=\frac{h_{CG}}{\sin (\theta )}$ و فاصله سطح آزاد مایع تا مرکز سطح دریچه$h_{CG}=$

مولفهٔ y مرکز سطح$\overline{Y}=$ و مولفه x مرکز سطح$\overline{X}=$

فرض:فشار هوا را صفر در نظر می گیریم. در واقع تمامی مولفه های فشار نسبی است.

کلیه نیروهای وارد برسطح دریچه ناشی از سیال بالای آن( مایع درون ظرف) را می توان در هنگام انجام محاسبات در یک نقطه منحصر به فرد تحت عنوان نیرویF معادل سازی نمود که این نقطه مرکز فشار (cp) نامیده می شود

الگو:چپ‌چین $F=P_{CG}A=\gamma h_{CG}=\rho g{h}_{CG}=.8\times {10}^3\times 9.806\times 4\sin (30)\times \frac{3\times 2}{2}=47068.8N$

درشکل زیر نقطهٔ k محل مرکز فشار روی سطح دریچه(cp) رانشان می دهد که نیروی F به این نقطه وارد می شود.

پرونده:12345678.png

ب) بر اساس قضیه محورهای موازی داریم:

الگو:چپ‌چین $I_{xx}={\overline{I}}_{xx}+A{\overline{y}}^2$

$I_{xy}={\overline{I}}_{xy}+A\overline{x}\overline{y}$

ابتدا حالت کلی زیر را بررسی می کنیم:

الگو:چپ‌چین $I_{xy}={\overline{I}}_{xy}=\frac{b(b-2s)L^2}{72}$

الگو:پایان چپ‌چین باتوجه به شکل زیر می بینیم که: L=a

همچنین باتوجه به شکل چون محور مختصات در مرکز سطح مثلث قرار داردپس:$\overline{X}=0$ و $\overline{Y}=0$

پرونده:Yousefi2.png

حال دریچهٔ مثلثی متساوی الساقین موجود در مسئله را بررسی می کنیم.از آنجا که مرکز سطح رو محور تقارن قرار میگیردپس در اینجا s و d باهم برابر وهر دو مساوی $\frac{b}{2}$ هستند.

پرونده:Yousefi1.png

$X_{cp}=\frac{\gamma \sin (\theta )I_{xy}}{p_{CG}A}=\frac{I_{xy}\sin (\theta )}{h_{CG}A}=\frac{I_{xy}}{\overline{Y}A}=\frac{{\overline{I}}_{xy}+\overline{X}\overline{Y}A}{\overline{Y}A}\Rightarrow X_{cp}=\overline{X}+\frac{{\overline{I}}_{xy}}{\overline{Y}A}$

الگو:پایان چپ‌چین باتوجه به شکل بالا و با توجه به فرمول زیر و در واقع به علت تقارن داریم:

الگو:چپ‌چین ${\overline{I}}_{xy}=\frac{b(b-2\frac{b}{2})L^2}{72}=0$ الگو:پایان چپ‌چین

الگو:چپ‌چین ${\overline{I}}_{xy}=0\Rightarrow X_{cp}=\overline{X}=\frac{2}{3}m=0.67m$ الگو:پایان چپ‌چین

الگو:چپ‌چین

$Y_{cp}=\frac{\gamma \sin (\theta )I_{xx}}{p_{CG}A}=\frac{I_{xx}\sin (\theta )}{h_{CG}A}=\frac{I_{xx}}{\overline{Y}A}=\frac{{\overline{I}}_{xx}+{\overline{Y}}^{2}A}{\overline{Y}A}\Rightarrow Y_{cp}=\overline{Y}+\frac{{\overline{I}}_{xx}}{\overline{Y}A}$

با توجه به رابطه بدست آمده به طور قطع مرکز نیرو(مرکز فشار) پایین تر از مرکز سطح قرار دارد

از طرفی با توجه به شکل بالا ممان اینرسی(${\overline{I}}_{xx}$)به علت تقارن دو برابر ممان اینرسی هریک ازمثلث ها در دو طرف محور تقارن حول محورx است

الگو:چپ‌چین

${\overline{I}}_{xx}=\frac{1}{12}a{\left(\frac{b}{2}\right)}^3+\frac{1}{12}a{\left(\frac{b}{2}\right)}^3$

$Y_{cp}-\overline{Y}=\frac{{\overline{I}}_{xx}}{\overline{Y}A}=\frac{2\times \frac{2\times {1.5}^3}{12}}{4\times \frac{3\times 2}{2}}=0.09375m\Rightarrow Y_{cp}=4+0.09375=4.09375m$

الگو:پایان چپ‌چین ج) گشتاور نیروهای وارد بر سطح دریچه (شامل نیروهایFوp وصرف نظر ازجرم) حول لولای CDرا برابر صفر قرار میدهیم

الگو:چپ‌چین $\sum _{}^{}M=0\Rightarrow p\times 2-F\times \frac{2}{3}=0\Rightarrow$ $p\times 2=F\times \frac{2}{3}\Rightarrow p\times 2=47068.8\times \frac{2}{3}\Rightarrow p=15689.6N$

---

نیروی وارد بر سطوح منحنی

در رابطه با سطوح منحنی ما مستقیما نمیتوانیم نیروهای وارد بر آن را محاسبه کنیم بلکه ابتدا باید به طور جداگانه مولفه های افقی و قائم را محاسبه و در نهایت با جمع برداری آنها نیروی کل را به دست اوریم. که به صورت زیر می‌باشد:

الف) مولفه افقی

برای محاسبه این مولفه باید نیروی وارد بر سطوح قایمی که از تصویر کردن منحنی در جهت عمود بر آن نیرو به دست می آید.

$F_H=\gamma h_{CG}{A}_H$

خط اثر این مولفه مرکز فشار روی تصویر سطح است.

ب) مولفه قائم

مقدار این مولفه برابر است با وزن مایع فرضی یا واقعی بر سطح منحنی

$F_V=\gamma V$

که منظور از حجم فرضی حجمی است که در نبود دریچه بالای دریچه جمع می‌گردد. به طور مثال درشکل الف (که مایع زیر دریچه هست) حجم بالای دریچه همان حجم فرضی و در شکل ب (که مایع بالای دریچه هست) حجم بالای دریچه همان حجم واقعی در نظر گرفته می‌شود.

با استفاده از سوپر پوزیش یا جمع آثار و یا روابط ریاضی می توان اثبات کرد کرد که چه در حالت اول که مایع فرضی می گیریم و چه در حالت ثانویه که مایع واقعی می گیریم برآیند نیرو های افقی برابر است با نیروی شناوری که سیال به حجم مغروق جسم به سمت بالا وارد می کند.

محل اعمال این مولفه مرکز حجم ستون مایع واقعی یا فرضی بالای سطح منحنی است.

در نهایت نیروی برآیند را از جمع برداری دو مولفه به دست می آوریم.

$F_R=\sqrt{{F_V}^2+{F_H}^2}$

برای تعیین مرکز فشار نیروی افقی از تصویر این نیرو بر صفحه قایم استفاده می کنیم و برای تعیین مرکز فشار نیروی قایم مرکز حجم سیال بالای سطح را تعیین می کنیم.

پرونده:Z.m1.png

$\begin{array}{cc}& \underset{A}{\int }d\overrightarrow{F}=-\int Pd\overrightarrow{A}\\ & \\ & F_x=-\underset{A}{\int }pd\sin \theta \\ & F_Y=-\underset{}{\int }Pd\cos \theta \\ & 1)F_x=F_H\\ & 2)F_Y=F_V+W\\ & \\ & 1)F_X=F_H\\ & 2)F_Y={F_V}^{/}-W^{/}\\ & {F_V}^{/}=F_V+(W+W^{/})\\ & {F_V}^{/}=P_{1}AV\\ & F_V=P_{2}AV\\ & W+W^{/}=\gamma hA\\ & {F^{/}}_V-F_V=(P_2-P_1)A=\gamma hA=W+W\\ \end{array}$

الف) پرونده:Z.m3.png

ب) پرونده:Z.m2.png